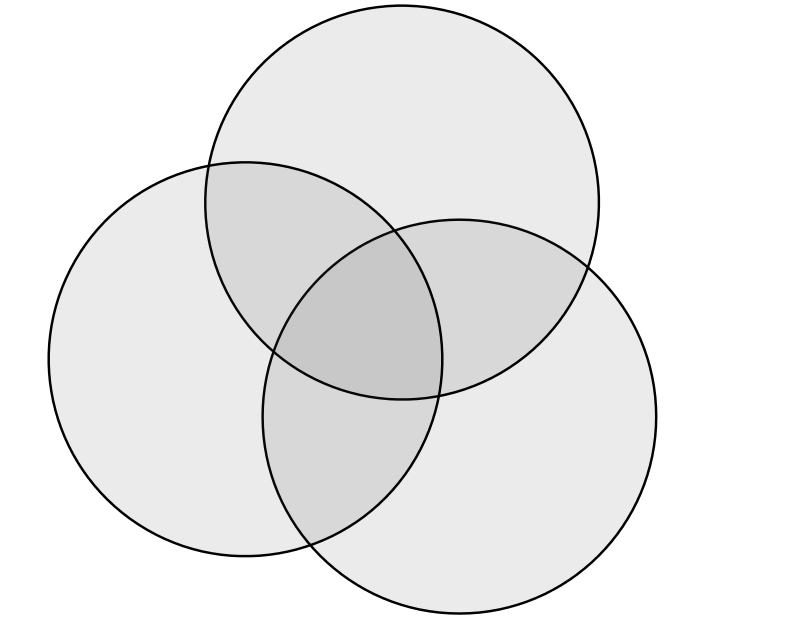
N個の集合のベン図が描けること

同僚に N個の集合のベン図 を描くスクリプト渡したらTwitter でちょっとバズったみたいなので解説を書きます。

N個の集合のベン図をかけるかという話で盛り上がってたら同僚がN個のベン図を描くスクリプトを作ってくれたので10個の集合のベン図貼っときますね． pic.twitter.com/ItoJQE45BT
— しえら@１日目東キ17a (@sierrarries) 2017年12月19日

本解説では、Nベン図の構成方法と、本当にベン図になっていることの証明の流れを解説したいと思います。

また、上記ツイートのソースコードはここ↓に置いておきます。 github.com

ブログも年1回くらいは更新しないとね。

ベン図

ベン図とは、みなさんご存知の、丸(閉曲線)の重なりから集合の部分集合や共通部分を説明するための図です。

ここでは、ベン図を以下のように定義します。

定義: ベン図

平面 $\mathbb{R}^{2}$ 上の単純閉曲線(自己交差しない閉曲線)のN元集合 $S=\{c_n\}_{n=1,\cdots,N}$ は、次の条件を満たすとき、Sを、N個の集合のベン図、もしくはN-ベン図であるという。

平面の各点xについて、xを囲む曲線の組み合わせによって平面を色分けした時、全ての組み合わせに対応する色が1度ずつ現れる。

閉曲線は互いに点で交わり、1点で交わる曲線は高々2本である。

1 は、もう少し正確に述べると、次のようになります。*1

平面からSのべき集合への関数 $f:\mathbb{R}^{2} \to 2^{S},\; f(x)= \left\{ c \in S \middle | x \in \mathrm{int}(c) \right\}$ が全射で、なおかつ、任意の $y \subset S$ について、yの $f$ による逆像が単連結

2 は、本来のベン図の定義には必要無いですが、図形をシンプルにするために課しておきます。

また、ここでは、回転対称性や、各閉曲線が凸であるという条件は課さないものとします。

閉曲線が円の場合N≦3まで, 楕円の場合N≦4までしかベン図を描くことができないそうです。また、回転対称なベン図は、Nが素数のときに限られるらしいです。ここでは、より一般の、対称性が低くてもいいので任意のNについてベン図を描くことを目標とします。

それでは、任意の自然数Nについて、Nベン図を描いていきましょう。

ベン図の双対グラフとハミルトン閉路

まずは準備のために、まずは、以下の補題を証明します。

補題 1

N ベン図の双対グラフにハミルトン閉路が存在するなら、N+1 ベン図が存在する。

ベン図の双対グラフとは、ベン図の線で区切られた各領域に1つずつ点(ノード)を描き、線1本を隔てる2つの領域の間に辺(エッジ)を結ぶことで得られる無向グラフのことです。

例えば、下図の青線で表される2-ベン図の双対グラフとは、黒丸のノードおよび黒線のエッジで表されるグラフです。

f:id:nunuki:20171231151949p:plain:w300

また、3-ベン図の双対グラフは次のようになります。

f:id:nunuki:20171231152152p:plain:w300

ハミルトン閉路とは、グラフの全てのノードを1度ずつ通る閉路のことです。

例えば、2-ベン図の双対グラフは、次のようなハミルトン閉路を持ちます。 (グラフ全体がハミルトン閉路になっています)

f:id:nunuki:20171231152331p:plain:w300

ここで、描かれたハミルトン閉路を新たな閉曲線とすると、3-ベン図ができます。

f:id:nunuki:20171231152421p:plain:w300

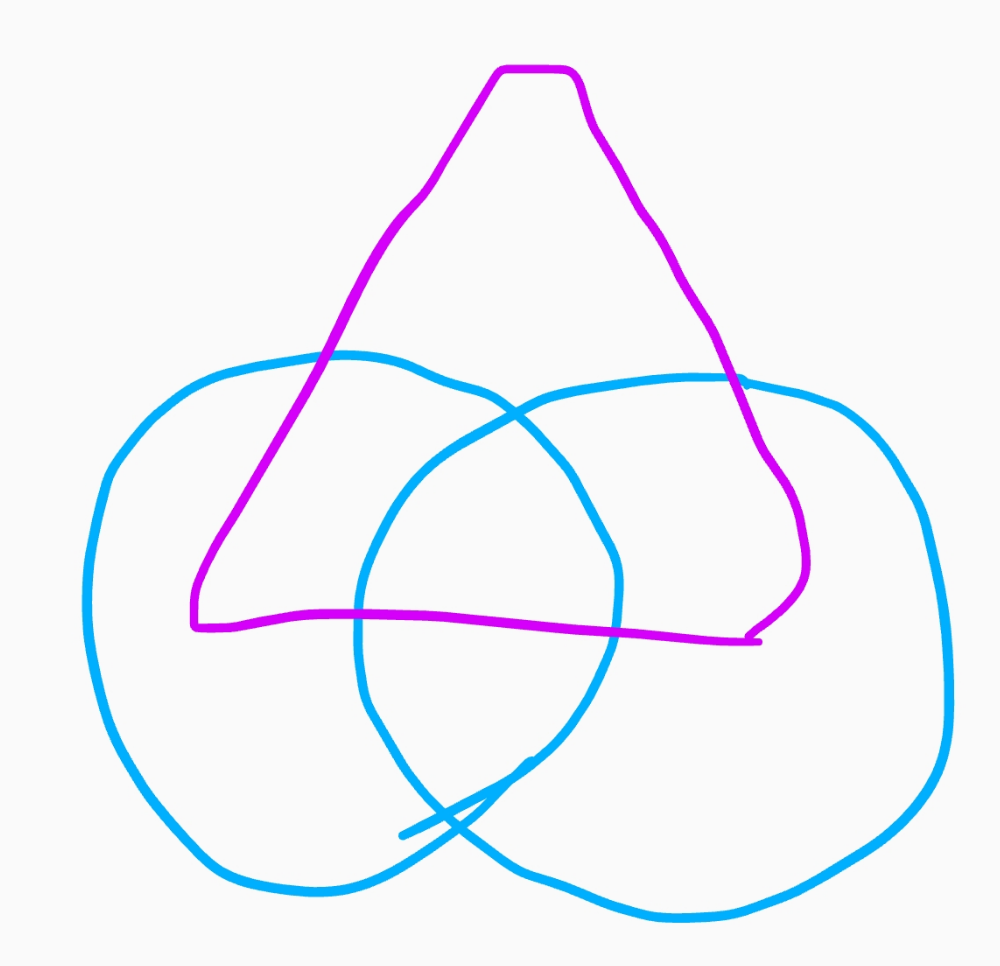
また、3-ベン図の双対グラフは、次のようなハミルトン閉路を持ちます。

f:id:nunuki:20171231152346p:plain:w300

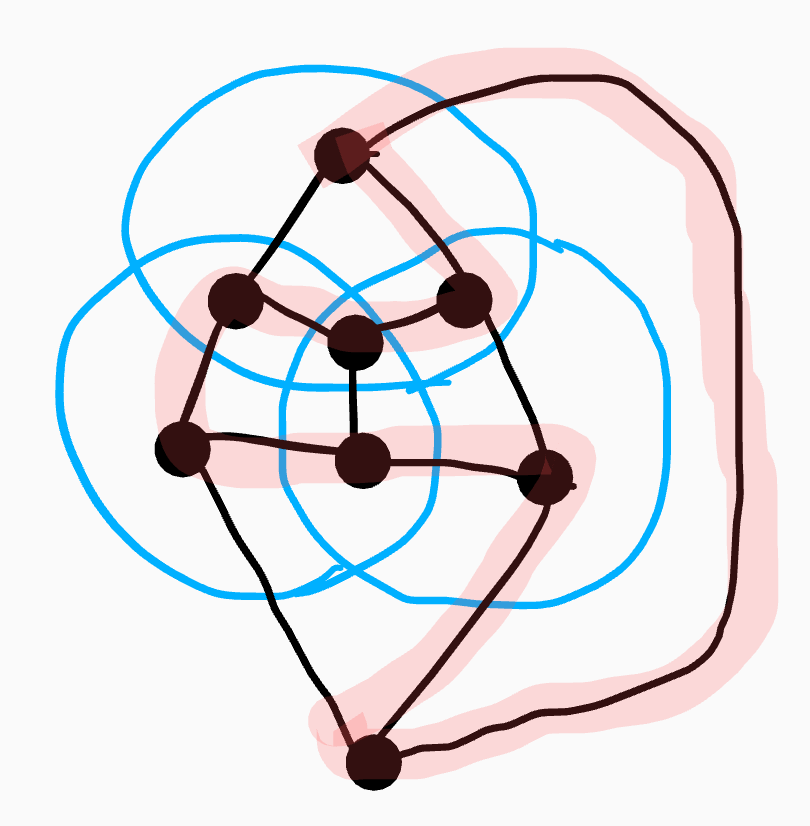
再び、ハミルトン閉路を新たな閉曲線とすると、4-ベン図ができます。

f:id:nunuki:20171231152443p:plain:w300

このように、Nベン図の双対グラフにハミルトン閉路が存在するとき、そのハミルトン閉路を新たな閉曲線とすると、N+1ベン図ができます。

なぜなら、Nベン図の双対グラフのハミルトン閉路は、 Nベン図の $2^{N}$ 個の領域を必ず1度ずつ通ります。このため、ハミルトン閉路は $2^{N}$ 個の各領域を2つに分割し、一方はハミルトン閉路の内側、もう一方は外側になります。したがって、ハミルトン閉路を追加することによって平面が各々異なる $2^{N+1}$ 個の領域に分割されることになり、 N+1ベン図ができることがわかります。

このように、Nベン図の双対グラフがハミルトン閉路を持つ場合、ハミルトン閉路を新たな閉曲線とすることで、 N+1 ベン図が得られることがわかりました。

問題は、このようなハミルトン閉路が、常に描けるかどうかです。

実は、一般のグラフが与えられたとき、そのグラフにハミルトン閉路が存在するか否かを判定する問題は、ハミルトン閉路問題と呼ばれ、NP完全という難しい(と信じられている)問題のクラスに属します。 *2

しかし、今対象としているのは一般のグラフではなく、 Nベン図の双対グラフという特殊な場合ですから、ハミルトン閉路が存在することを証明することができます。

このことを証明するために、「グレイコード」の性質を用います。

グレイコード

先ほどのNベン図の各領域に名前を付けます。ここでは、閉曲線の内側にあるならば1 外側ならば0を閉曲線の数だけ並べることで、各領域にN桁の2進数を対応させます。

例えば、3ベン図の各領域に名前をつけると、次のようになります。

f:id:nunuki:20171231153434p:plain:w300

ここで、1本の線で隔てられた2つの領域の数は、 2進表記の1桁だけが異なっていることがわかります。

つまり、先ほどの双対グラフのハミルトン閉路が通る領域の数を並べると、隣り合った数字が、2進表記の1桁だけが異なるような数列が出来上がります。

さて、ここで、グレイコード(Gray code) を導入します。

グレイコード $G_{n}$ とは、2進数の数列で、次の2つの条件を満たすものです。

$G_{n}$ には、2進表記n桁で表される $0 \sim 2^{n}-1$ の全ての数字が一度づつ現れる。
数列の隣り合った*3数字は、2進表記で1つの桁だけが異なる。

例えば、 $G_3$ は次のような長さ8の数列です。

これは、まさに、双対グラフのハミルトン閉路から作った数列と同じ形をしています！

以上のように、ベン図の双対グラフのハミルトン閉路がグレイコードに対応していることがわかりましたが、ここでは、逆に、グレイコードの性質を使うことで、実際にハミルトン閉路が引けることを証明したいと思います。

そのために、まずは、グレイコードのいくつかの性質を見ていきましょう。

グレイコードは、次のように再帰的に作ることができます。まず、 $G_{n}$ の各項を2回ずつ繰り返した、2倍の長さの数列を考えます。

次に、出来上がった数列の各数の右端に、0, 1, 1, 0, 0, 1, 1, ... を追加していくと、 $G_{n+1}$ ができます。

構成のしかたから明らかなように、 $m \leq n$ のとき、 $G _ {n+1}$ の各数の左からm桁目を集めた数列は、 $G _ {n}$ の各数の左からm桁目を集めた数列を2倍の長さにしたものになっています。

例えば、 $G_{3}$ の左から2桁目を縦に読むと、

[0,0,1,1,1,1,0,0,0]

ですが、 $G_{4}$ の場合、

[0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0]

となります。このように、 $G_{n}$ のm桁目の数字を集めた数列は、 nが変化しても、長さが変わるだけで、中身は本質的に変わりません。

ここで、この数列を横方向に縮め、連続区間 [0,1) で定義された関数 $g_{m}(x)$ で表します。つまり、

$g _ {m}(x) = \lim _ {n \rightarrow \infty } (G_{n}) _ { \lfloor 2^{n-1} x \rfloor }$

とします。

それでは、このグレイコードを使って実際にN-ベン図を構成していきましょう。

N-ベン図の構成

定理: N-ベン図の存在

実数 $\delta _ {1}, \cdots, \delta _ {N}$ が、 $1 > \delta _ {1} > \delta _ {2} > \cdots > \delta _ {N-1} > \delta _ {N} > 0$ を満たすとき、次の極座標表示で表される曲線 $C _ {1}, \cdots, C _ {N}$ はN-ベン図を成す。

$C _ {n}: r = 1 + \left(2g _ {n} \left( \frac {\theta} {2\pi} \right) - 1 \right) \delta _ {n} \;\;\; \cdots (1)$

ただし、非連続となる部分は動径方向に線分を引くことで連続な閉曲線にするものとする。

$C _ {n}$ の形は次のようになります。

f:id:nunuki:20171231155023p:plain 赤点線は半径1の円(単位円)です。

n が大きくなるなるにつれて、歯車型の曲線の歯の数が増え、歯の長さ(切込みの深さ)が小さくなっています。

各歯車は、グレイコードの1に対応する部分が出っ張って(半径が $1+\delta _ {n}$ )おり、 0に対応する部分が凹んで(半径が $1-\delta _ {n}$ )います。

これらを重ねることで、冒頭のツイートの図になります。

f:id:nunuki:20171231161217p:plain

ここで、赤点線で描いた単位円上のある一点を考えると、閉曲線のうち、出っ張っている物の内側、凹んでいる物の外側になっています。

例えば、図中の点Pは、 $C _ {3}, C _ {4}$ の内側、 $C _ {1}, C _ {2}, C _ {5}$ の外側になっています。

点Pを単位円周上で動かすと、グレイコードの性質から、内側・外側の全ての組み合わせが1回ずつ現れることがわかります。

つまり、上述の式(1) で表される図形がNベン図になっている場合、単位円は全ての領域を1度ずつ通る経路、すなわち、双対グラフのハミルトン閉路になっていることがわかります。

よって、補題1により、 $\{ C _ {1}, \cdots, C _ {N} \}$ がN ベン図になっているとき、これに単位円を追加したものはN+1 ベン図になっています。

ここで、N+1 個目に追加する図形は単位円でなくても、単位円に近い図形を選ぶことができます。

実際、単位円の代わりに $C _ {N+1}$ を追加する場合を考えると、 $0 \lt \delta _ {N+1} \lt \delta _ {N} \lt \cdots \lt \delta_ {1}$ ですから、 $C _ {N+1}$ の出っ張っている部分も凹んでいる部分も常に $C _ {1}, \cdots, C _ {N}$ より単位円に近いことになります。

したがって、 $C _ {N+1}$ は、単位円と同じ位置θ、つまり、 $C _ {1}, \cdots, C _ {N}$ が動径方向に変化している位置(凸凹の切り替わり = グレイコードの0と1の切り替わりの位置)でのみ $C _ {1}, \cdots, C _ {N}$ と交わることとなり、単位円の場合と同様の議論が可能です。

以上のことから、 $\{ C _ {1}, \cdots, C _ {N} \}$ がNベン図のとき、 $\{ C _ {1}, \cdots, C _ {N+1} \}$ もN+1ベン図であることが言えました。

1つの閉曲線は明らかに1-ベン図ですから、任意のNについて、 $\{ C _ {1}, \cdots, C _ {N} \}$ がベン図となっていることがわかりました。

まとめ

Nベン図からN+1ベン図を作る問題を、双対グラフのハミルトン閉路問題に帰着した。
グレイコードを使って、常にハミルトン閉路が描けるようなベン図を構成した。

*1: $\mathrm{int}(c)$ は単純閉曲線 $c$ の内部とする

*2:もし、ハミルトン閉路問題を多項式時間で解くアルゴリズムができた場合、全ての暗号通信が傍受可能になってしまうだけでなく、暗号通貨が盗み放題になってしまします。一方、ハミルトン閉路問題を多項式時間で解くアルゴリズムが存在しないことを証明した場合、アメリカのクレイ数学研究所から懸賞金の100万ドルがもらえます

*3:数列の末尾と先頭も隣り合っているものとする。

ベン図

定義: ベン図

ベン図の双対グラフとハミルトン閉路

補題 1

グレイコード

N-ベン図の構成

定理: N-ベン図 の存在

まとめ

定理: N-ベン図の存在