2018-12-15

異空間散歩！双曲空間を歩いてみよう。

この記事は、scouty Advent Calendar の14日目です。

本記事には、線の束がウネウネ動くgif動画があります。人によっては気持ち悪いと感じるかもしれませんので、苦手な方はご注意ください。

f:id:nunuki:20181215054133p:plain

双曲空間埋め込み - Poincaré Embedding

近年、機械学習界隈で双曲空間(Hyperbolic geometry) への埋め込み(Poincaré Embedding; Nickel & Kiela, 2017)¹が流行っています。双曲空間は、ユークリッド空間(普通のN次元空間)と異なり、原点から遠ざかるに連れて(正確な表現ではありませんが)急激に空間が拡がるという性質を持っています。このため、ユークリッド空間では不可能であった『木構造の埋め込み』が双曲空間においては可能となる²など、少ない次元でより複雑な構造を扱うことができる点が注目されています。今年のICML でも(Octavian et al., 2018)³ や (Nickel et al., 2018)⁴ などの最新手法が提案され、ますます盛り上がりを見せています。

双曲空間への埋め込みについては、日本語だとこちらのブログが詳しいです。また、scouty でもやってみた記事を出したりしてます。

今回は、「双曲空間には木構造をはじめとする複雑な構造を埋め込むことができる」ことを直感的に理解するために、双曲空間に作られた迷路を歩いてみましょう。

ポアンカレ円盤モデル

以降では、2次元の双曲空間のみを考えます。

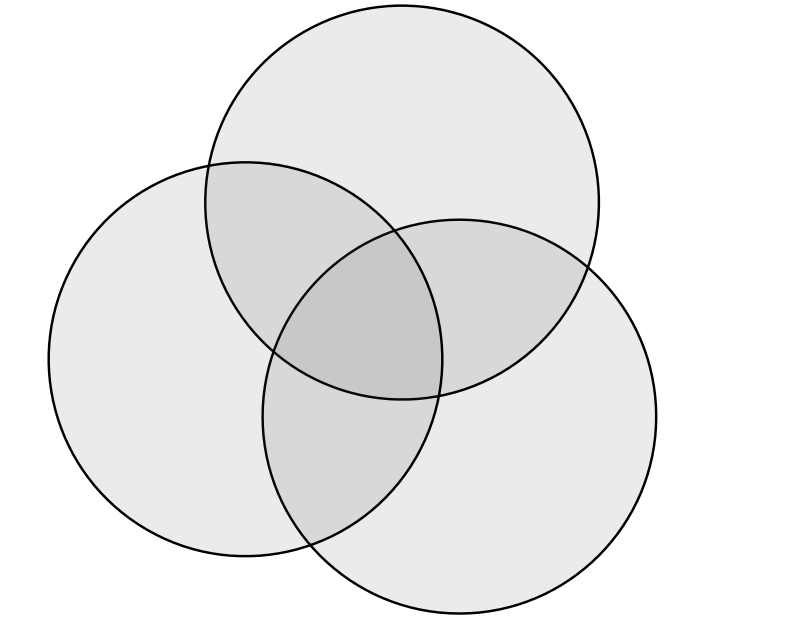
まずは、通常のユークリッド空間に埋め込むことができない双曲空間をイメージするために、ポアンカレの円板モデルを導入します。ポアンカレ円板とは、双曲空間を表現するモデルの1つです。双曲空間を表すモデルはいくつもありますが、ポアンカレ円板モデルは数理的な解析がしやすいなどの理由から、双曲空間への埋め込みの研究の多くでこのモデルが採用されています。

図1: ポアンカレ円板モデル

ポアンカレ円板は双曲空間の局所座標の1つと考えることもできます。いま、双曲空間の地図を書くことを考えます。双曲空間は通常の２次元平面(ユークリッド空間)に長さと角度を保ったまま埋め込むことはできません。そこで、長さと角度のどちらかは崩れてしまいますが、投影法を駆使して2次元の平面に地図を描きます。これは、ちょうど、地球の表面(球面)の地図をメルカトル図法や方位図法などの投影法によって平面に描いていることに似ています。

双曲空間のポアンカレ円板モデルは、地球の地図における方位図法に相当する投影法であると言えます。図2は、東京を中心とする(正距)方位図法で描かれた世界地図です。この地図では、東京と別の都市(例えばマイアミ)とを結ぶ最短経路は直線(赤線)で描かれます。地球の表面に沿った線をこのまま"まっすぐ"伸ばして行くと、地球を一周して東京に戻ってきます(青線)。この「地球上の2点を結ぶ最短経路」は、地球の表面を ”まっすぐ” 走る車の軌跡であるとも言えます。このように、球面のような曲がった面を "まっすぐ" 進むことでできる軌跡を測地線と呼びます。球面の測地線は、球面を球の中心を通る平面で切った輪切りの円(大円)になります。

f:id:nunuki:20181215054254p:plain — 図2: 東京を中心とする正距投影図法で描かれた世界地図

下図3の赤線は、ポアンカレ円板モデルにおける中心点を通る測地線(赤線)を表しています。球面の方位図法と同様に、中心を通る測地線は直線で表されます。ただし、双曲空間は球面と違って閉じていないので、どんなにまっすぐ進んでも元の点に戻ってくることはありません。つまり、図3の円の上下左右は繋がっておらず、ポアンカレ円板の外側の半径1の円は、双曲空間の無限遠点を表します。

f:id:nunuki:20181215054516p:plain — 図3: ポアンカレ円板モデルにおける、原点を通る測地線(赤)と原点からの等距離線(青)

図3の青い円は、中心からの距離が一定の線(つまり、ポアンカレ空間における"円")を等間隔で表しています。中心点を離れるにつれて、円が詰まってい流のがわかります。これは、中心から離れるとどんどん縮尺が小さくなり、円板の端では縮尺が無限小になっていることを表しています。このことは、図2において、中心から離れた点で縮尺が大きくなっている(例えば、南米大陸が非常に大きく伸びている)ことを考えると、対照的です。

ポアンカレ円板において、中心を通る測地線は直線で表されましたが、中心以外を通る測地線は、端の円と直交する円弧になります。中心以外の点を通る測地線の様子を図4に示しました。

f:id:nunuki:20181215054643g:plain — 図4: ポアンカレ円板における平行移動

ポアンカレ円板モデルのもう1つの大事な性質として、双曲空間における2つの線のなす角度は、ポアンカレ円板における角度と等しいという性質(正角性)があります。実際、図4では、赤い線と青い線は、平行移動しても常に直交していることがわかります。

「直進、右折」を繰り返す

ポアンカレ円板を導入して、双曲空間を歩く準備ができました。しかしその前に、通常の平面や、球面を歩いた場合にどうなるかを復習しておきます。

あなたは通常の2次元平面の点Aに立っているとします(図5a)。そこから、あなたはある距離(例えば100m)を真っ直ぐ歩き、次に90度回れ右をし、また同じだけ(100m)歩き、、と繰り返した場合どうなるでしょうか？もちろん、この操作を4回繰り返すと、正方形を描いて元の位置に戻ります。

f:id:nunuki:20181215054759j:plain — 図5: 平面と球面上で、直進と右折を繰り返す。

しかし、球の場合には平面と異なり、直進と右折を、4回ではなく3回や2回繰り返すだけで元の点に戻ることが可能です。図5b のように、北極点からスタートして、赤道まで歩き、90度回って赤道上を同じだけ歩き、さらに90度回って同じだけ歩くと、3回の繰り返しで北極に戻ってきます。さらに、図5c のように、北極をスタートしてから南極まで歩き、そこで90度回ってまた同じだけ歩くと、元の北極点に戻ってきます。

それでは、双曲空間の場合、何回で戻ってくることができるでしょうか？結論から言うと、戻ってくるのには、直進と右折を4回よりも多い回数繰り返す必要があります。さらに、直進する距離がある程度以上長くなると、何回繰り返しても元の位置に戻らないことすらありえます。このように「直進と右折を何度繰り返しても元の位置に戻らない」という性質が、実は「双曲空間に木構造を埋め込むことができる」ということと深く関連しているのです。

双曲空間の迷路を歩く

まずはこちらのgif動画をご覧ください。

f:id:nunuki:20181215054837g:plain — 図6: 双曲空間の迷路を歩く

これは、双曲空間に無限に広がる迷路の中を進む様子をポアンカレ円板に投影した図です。現在地から遠い点は、ポアンカレ円板に投影することによって歪んでしまっていますが、双曲空間において、迷路を構成している四角いタイルは全て同じ形で、すべての道はまっすぐ(測地線)で、すべての十字路は直交しています。

図6は、一本道では直進し、分かれ道(十字路)では常に右に90度回転していますが、平面や球面の場合とは異なり、一度訪れた場所に２度と訪れることはありません。さらに、一度、ある分かれ道で「右折」を選ぶと、その分かれ道で「直進」や「左折」することでたどり着ける場所にたどり着くためには、この分かれ道まで戻ってくる以外に方法が無いこともわかります。つまり、迷路の中の分かれ道をノード、分かれ道を繋ぐ通路をエッジとするグラフ構造を考えると、スタート地点を根とすると、1つのノードが、「直進」「右折」「左折」の3つのノードを子として持つ木構造になっていることがわかります。さらに言えば、これらのエッジはすべて同じ長さであり、すべてのノードは等価であることもわかります。このように、双曲空間を用いることで、エッジの長さを保ったままグラフ構造を埋め込むことができることがわかりました。

まとめ

Poincaré Embedding など、巷で流行っている双曲空間を理解するため、ポアンカレ円板による可視化を行いました。ユークリッド平面や球面と比較して、双曲空間は無限に「直進、右折」を繰り返しても元の点にたどり着かないことが起こりうることを説明しました。このことが、「双曲空間に木構造を埋め込める」ということと深く関係していることを説明しました。

なお、作図に用いたスクリプトは一応こちらにおいておきます。

余談

図6の迷路のような構造を持った格子を(配位数4の)Bethe格子と呼んだりします。ユークリッド空間では実現不可能ですが、木構造を持っているため、諸々の解析がしやすく、物性物理において格子系を研究する際の toy model としてよく使われたりします。

参考文献

https://arxiv.org/abs/1705.08039 ↩
これは、「初等的でない双曲群が階数2の自由群を含む」という事実からもわかります。京大の藤原先生の講義ノート「双曲群の手引き(1995)」にその証明があります(定理3.2)。 ↩
http://proceedings.mlr.press/v80/ganea18a.html ↩
http://proceedings.mlr.press/v80/nickel18a.html ↩

2018-03-04

パスワードを忘れないようにブログに書いておく。

セキュリティの問題で今まで躊躇してたMoneyForward をついに始めた。せめてものリスクを最小化するために、MFと銀行口座のパスワードを、推測できないランダムな文字列にすることにした。

しかしながら、Webサイトごとに異なるランダムな文字列を全て覚えるのは現実的ではないため、パスワードマネージャを用いる必要がある。主なパスワードマネージャには、次のような物がある:

ローカルのパスワードマネージャ (例: Mac の KeyChain など)
クラウドのパスワードマネージャ (例: 1Password など)

1 は、他のデバイスとパスワードが共有できないため、不便である。 2は、クラウドにパスワードを預けることはやはり漏洩のリスクが伴うし、クラウドサーバーが落ちるとログインできなくなってしまうおそれがあるなど、自分の手の届かないところが単一障害点となってしまうことが問題である。

そこで、

サイトごとのパスワードを、マスターパスワードとURLのハッシュで生成する
生成ロジックを、ブログ等で大々的に公開する

ことで、サーバーが落ちた場合でも、マスターパスワードから生成ロジックによってパスワードを再生成できるようにすることを考える。

パスワード生成スクリプトは↓に公開した¹。

Password Generator

マスターパスワードの作成

この方法で大切になるのはマスターパスワードの安全性である。人間、そこまでランダムな文字列というものは作れるものではないし、完全にランダムな文字列は覚えづらい。そこで、文字のマトリクスを作り、そこに図形を描いて覚えるようにする。

マスターパスワードの生成

任意の文字列(seed) を入力する。

seed のSHA256 ハッシュ値をBase64( RFC4648 )エンコードで求める。

得られたBase64文字列を7文字ずつ改行して 7×6+2 (最後の文字は=) のマトリクスを作る。

マトリクス上で図形を描き、描いた位置の文字を拾って、マスターパスワードとする。

seed の値は秘密にする必要はない。例えば、yyyymmdd形式で表した生年月日を用いる。

得られるマトリクスは、例えば、seedが空文字列の場合、次のようになる。

$ openssl dgst -sha256 -binary /dev/null | base64 | fold -7 | sed -e 's/./ &/g'
 4 7 D E Q p j
 8 H B S a + /
 T I m W + 5 J
 C e u Q e R k
 m 5 N M p J W
 Z G 3 h S u F
 U =

当然であるが、マトリクスの上に描く図形はなるべくランダムで覚えやすいものとする。私の場合、何故か覚えている子供の頃の実家のトイレの壁の汚れの模様を意匠化したものとした。 (実家のトイレはリフォームしたので、その壁の汚れはもう残っていない。)

マスターパスワードの長さは14文字以上にする。詳しくは後述する。

サイトごとのパスワードの生成

サイトごとのパスワードは、サイトのFQDN (URL の https://xxxx/bbb の xxx の部分) とマスターパスワードからハッシュ関数により生成する。

サイトパスワードの生成

HTTPS サイトのSSL証明書に記載されている FQDN を、マスターパスワードによって N=1000回 SHA-256 HMACをとる。

得られたハッシュ値をBase64 エンコードし、サイトで利用可能な最大長を超えない4の倍数の長さの部分文字列をパスワードとする。

このようにサイトのパスワードを作成することで、あるサイトのパスワードが漏洩した場合でも別のサイトのパスワードが推測されることはないうえ、マスターパスワードさえ忘れなければ何度でも再生成できる。

マスターパスワードの長さ

マスターパスワードは何文字以上が良いであろうか。あるサイトのパスワードが漏洩した場合でも、マスターパスワードや他のサイトのパスワードが実質的に漏洩しない安全性が必要である。

SHA-256 はBitcoin のPoWで使われていることでも有名である。つまり、SHA-256 ハッシュの計算量はマイニングパワーとして取引されており、「1ハッシュ=〇〇円」という値段がついている。

このサイトによれば、 1ギガハッシュ/秒で1週間マイニングすると、平均0.006559ドル(≒0.7円)の報酬が得られるという計算になる。つまり、ビットコインをマイニングすれば、1 [GH/s] ÷ 0.7[円/週] = $8.6 \times 10^{14}$ ハッシュごとに、約1円の報酬が得られることになる。

私の資産(高々数百万円)をリスクを犯して奪うために、1億円分の計算をすることは考えられないため、 $P = 8.6 \times 10^{14} \times 10^{8}$ 回のハッシュ関数を計算しなければ破れないパスワード長とすればよい。

seed によって異なるが、マトリクスに現れるunique な文字の種類は30種類程度なので、長さLのマスターパスワードは $30^{L}$ 通りである。サイトのパスワードを1回計算するのに、N=1000回のハッシュ計算が必要なので、

$30^{L} \times N \geq P$

$L \geq \log(P/N) / \log(30) \approx 13.5$

よって、マスターパスワードは14文字以上が安全である。

資産がもっと多いよって人は、 $\log_{10}(30) \approx 1.477$ なので、資産が3桁増えるごとにマスターパスワード長の下限を2文字増やすとよい。

このスクリプトは、ブラウザ上だけで動作し、最初にスクリプトをロードする以外には一切の通信を行わない。万全を期すためには、「プライベートブラウジング」モードで上記ページを開き、インターネット接続を切ったうえでパスワード生成を行い、ブラウザを閉じてから接続を再開すると良い。↩

2018-02-24

第4回ドワンゴからの挑戦状本選(オープン) 問題C

競プロにちょっと興味を持った。

最速が出たので解説します。

dwacon2018-final-open.contest.atcoder.jp

(0ベースで)上からi段, 左からj番目のブロックの数字を $a _ {i,j}$ とする。

                   +-----+
                   | a00 | 
             +-----+-----+-----+
             | a10 | a11 | a12 |
       +-----+-----+-----+-----+-----+
       | a20 | a21 | a22 | a23 | a24 |
 +-----+-----+-----+-----+-----+-----+-----+
 | a30 | a31 | a32 | a33 | a34 | a35 | a36 |
 +-----+-----+-----+-----+-----+-----+-----+

ここで、xor を $\oplus$ で表すと、頂点の数字は、

$a _ {0,0}= a _ {1,0} \oplus a _ {1,1} \oplus a _ {1,2}$

$\;\; = (a _ {2,0} \oplus a _ {2,1} \oplus a _ {2,2}) \oplus (a _ {2,1} \oplus a _ {2,2} \oplus a _ {2,3}) \oplus (a _ {2,2} \oplus a _ {2,3} \oplus a _ {2,4})$

のように展開していくことができる。 i回展開すると頂点の数字 $a _ {0,0}$ は $a _ {i,0}, \cdots, a _ {i,2i}$ によって表される。

xor 演算は結合的かつ交換的なので、 i回展開した式に $a _ {i,j}$ が現れる回数を $n _ {i,j}$ で表すと、

$\displaystyle a _ {0,0} = \bigoplus _ {j=0} ^ {2i} \bigoplus _ {n=1} ^ {n _ {i,j}} a _ {i, j}$

となるが、 $a \oplus a = 0$ なので、 $t _ {i,j} := {n _ {i,j}\, \mathrm{mod\,} 2}$ とすれば、

$\displaystyle a _ {0,0} = \bigoplus _ {j=0} ^ {2(N-1)} a _ {N-1, j} t _ {N-1,j} \;\; = \bigoplus _ {m=1} ^ {M} \bigoplus _ {j=P _ {m-1}} ^ {P _ {m}-1} v _ {m} t _ {N-1,j} \;\; = \bigoplus _ {m=1} ^ {M} v _ {m} \left( \bigoplus _ {j=P _ {m-1}} ^ {P _ {m}-1} t _ {N-1,j} \right)$

となる。ただし、 $P _ {m} = L _ {1} + \cdots + L _ {m}$ である。

よって、 $R _ {m} := \bigoplus _ {j=P _ {m-1}} ^ {P _ {m}-1} t _ {N-1,j}$ とすれば、 $a _ {0,0} = \bigoplus _ {m=1} ^ M (v _ {m} R _ {m})$ となり、 $R _ {m}$ は0 または1 なので、 m = 1,…,M について、 $R _ {m}$ が1となる全ての $v _ {m}$ のxor を取れば良い。

$S _ {i, p} := \bigoplus _ {j=0} ^ {p} t _ {i,j}$ とすれば、 $R _ {m} = S _ {P _ {N-1, m} - 1} - S _ {P _ {N-1, m - 1} - 1}$ なので、以下では、 $S _ {i, j}$ を求める。

$t _ {i, j}$ の漸化式

$a _ {i,j}$ は、 $a _ {i-1,j-2}, a _ {i-1,j-1}, a _ {i-1,j}$ に現れるため、 $n _ {i,j} = n _ {i-1,j-2} + n _ {i-1,j-1} + n _ {i-1,j}$ となるため、

$t _ {i,j} = n _ {i,j} \, \mathrm{mod} \, 2 = ( n _ {i-1,j-2} + n _ {i-1,j-1} + n _ {i-1,j} ) \, \mathrm{mod} \, 2 = t _ {i-1,j-2} \oplus t _ {i-1,j-1} \oplus t _ {i-1,j}$

という漸化式が得られる。

この漸化式を使ったDPによって、 $2N^{2}$ 個のブロックを上から順に $t _ {i,j}$ の値で埋めていくことができるが、 $N \leq 252,525 \times 10^{9}$ なので間に合わない¹。

そこで、 $t _ {i,j}$ フラクタル的な性質を用いる。

フラクタルを用いた漸化式

$t _ {i,j}$ を埋めていくと、シェルピンスキーのギャスケットのようなフラクタル図形が現れる。

f:id:nunuki:20180224195259p:plain

図の全体を半分のサイズに縮小すると、上半分の図形とほぼ重なる。

実際、

$t _ {2i, 2j} = t _ {2i - 1, 2j-2} \oplus t _ {2i - 1, 2j-1} \oplus t _ {2i - 1, 2j} = t _ {2(i-1), 2(j-2)} \oplus t _ {2(i-1), 2(j-1)} \oplus t _ {2(i-1), 2j}$

となり、 $t _ {2i, 2j}$ は $t _ {i, j}$ と同じ漸化式を満たすため、 $t _ {2i, 2j} = t _ {i, j}$ である。

また、 $t _ {2i, 2j+1} = 0$ である。これは、次のように示せる:

$n _ {i,j}$ は、 0段,0番のブロックから、左下、下、右下のいずれかに進むという操作を繰り返し、 i段,j番のブロックにたどり着く経路の本数を表す。各経路は、進む方向 {'l' (左下), 'r' (右下), 'c' (下)} を順に並べた文字列と一対一に対応する。 (i,j)にたどり着くためには、右下に進む回数と左下に進む回数の差が j-i に等しければよいため、対応する文字列の文字'r'の個数と'l'の個数の差はj-i である。 iが偶数、jが奇数であるとき、文字列に含まれる'c'の個数は奇数となるため、文字列の前半に含まれる'c'の個数と後半に含まれる'c'の個数は異なる。このため、任意の文字列sに、sを反転させた文字列s'を対応させると、 s' はs と異なる経路に対応する。よって、全ての文字列sには対応する文字列s' が存在するため、文字列の個数 $n _ {i,j}$ は偶数となり、 $t _ {i, j} = n _ {i,j}\, \mathrm{mod}\, 2 = 0$ である。

まとめると、i が偶数のとき、次のような漸化式が得られる。

$t _ {i,j} = \begin{cases} t _ {i/2, j/2}, \;\; j: \; \mathrm{even}, \\ 0, \;\; \;\; \;\; \;\; j: \; \mathrm{odd}. \end{cases}$

$S _ {i, j}$ の漸化式

i が偶数のとき、

$\displaystyle S _ {i, j} = \bigoplus _ {k=0} ^ {j} t _ {i,k} = \bigoplus _ {\substack{k=0 \\ k : \mathrm{even}}} ^ {j} t _ {i/2,k/2} = \bigoplus _ {k=0} ^ {\lfloor j/2 \rfloor} t _ {i/2,k} = S _ {i/2, \lfloor j/2 \rfloor}$

i が奇数のとき、

$\displaystyle S _ {i, j} = \bigoplus _ {k=0} ^ {j} t _ {i,k} = \bigoplus _ {k=0} ^ {j} (t _ {i-1,j-2} \oplus t _ {i-1,j-1} \oplus t _ {i-1,j}) \\ \displaystyle = S _ {i-1,j-2} \oplus S _ {i-1,j-1} \oplus S _ {i-1,j} \\ \displaystyle = S _ {(i-1)/2,\lfloor (j-2)/2 \rfloor} \oplus S _ {(i-1)/2,\lfloor (j-1)/2 \rfloor} \oplus S _ {(i-1)/2,\lfloor j/2 \rfloor} \\ \displaystyle = \begin{cases} S _ {(i-1)/2,\lfloor j/2 \rfloor - 1}, \;\; j: \mathrm{odd}, \\ S _ {(i-1)/2,\lfloor j/2 \rfloor}, \;\;\;\; j: \mathrm{even}. \end{cases}$

まとめると、任意のi,j について、

$\displaystyle S _ {i, j} = \begin{cases} S _ {\lfloor i/2 \rfloor, \lfloor j/2 \rfloor - 1}, \;\; ij: \mathrm{odd}, \\ S _ {\lfloor i/2 \rfloor, \lfloor j/2 \rfloor}, \;\;\;\; \mathrm{otherwise}. \end{cases}$

この漸化式を使うことで、 $S _ {N-1, j}$ を再帰的に $\mathcal{O} (\log N )$ で計算できる。

よって、全体の計算量は $\mathcal{O} (M \log N )$ 。

実装は以下。

dwacon2018-final-open.contest.atcoder.jp

#include <vector>
#include <iostream>
using namespace std;
 
#define LL long long
 
inline LL S(LL p, LL q){
  while(true){
    if(q<0) return 0;
    if(p==0) return 1;
    q = (q>>1) - (p&q&1);
    p = p>>1;
  }
}
 
void solve(long long M, vector<long long> v, vector<long long> L){
  LL N = 0;
  for(LL m=0; m<M; m++) N += L[m];
  LL p=(N-1)>>1;
 
  LL rst=0, q=-1, prevS=S(p, q);
  for(LL m=0; m<M; m++){
    q += L[m];
    LL nextS = S(p, q);
    if(nextS != prevS) rst ^= v[m];
    prevS = nextS;
  }
  cout << rst << endl;
}
 
int main(){ 
    long long M;
    scanf("%lld",&M);
    vector<long long> L(M-1+1);
    vector<long long> v(M-1+1);
    for(LL i = 0 ; i <= M-1 ; i++){
        scanf("%lld",&v[i]);
        scanf("%lld",&L[i]);
    }
    solve(M, v, L);
    return 0;
}

実は、これでも頑張れば間に合うらしい: kmyk 氏の解答 ↩

2017-12-31

N個の集合のベン図が描けること

同僚に N個の集合のベン図 を描くスクリプト渡したらTwitter でちょっとバズったみたいなので解説を書きます。

N個の集合のベン図をかけるかという話で盛り上がってたら同僚がN個のベン図を描くスクリプトを作ってくれたので10個の集合のベン図貼っときますね． pic.twitter.com/ItoJQE45BT
— しえら@１日目東キ17a (@sierrarries) 2017年12月19日

本解説では、Nベン図の構成方法と、本当にベン図になっていることの証明の流れを解説したいと思います。

また、上記ツイートのソースコードはここ↓に置いておきます。 github.com

ブログも年1回くらいは更新しないとね。

ベン図

ベン図とは、みなさんご存知の、丸(閉曲線)の重なりから集合の部分集合や共通部分を説明するための図です。

ここでは、ベン図を以下のように定義します。

定義: ベン図

平面 $\mathbb{R}^{2}$ 上の単純閉曲線(自己交差しない閉曲線)のN元集合 $S=\{c_n\}_{n=1,\cdots,N}$ は、次の条件を満たすとき、Sを、N個の集合のベン図、もしくはN-ベン図であるという。

平面の各点xについて、xを囲む曲線の組み合わせによって平面を色分けした時、全ての組み合わせに対応する色が1度ずつ現れる。

閉曲線は互いに点で交わり、1点で交わる曲線は高々2本である。

1 は、もう少し正確に述べると、次のようになります。*1

平面からSのべき集合への関数 $f:\mathbb{R}^{2} \to 2^{S},\; f(x)= \left\{ c \in S \middle | x \in \mathrm{int}(c) \right\}$ が全射で、なおかつ、任意の $y \subset S$ について、yの $f$ による逆像が単連結

2 は、本来のベン図の定義には必要無いですが、図形をシンプルにするために課しておきます。

また、ここでは、回転対称性や、各閉曲線が凸であるという条件は課さないものとします。

閉曲線が円の場合N≦3まで, 楕円の場合N≦4までしかベン図を描くことができないそうです。また、回転対称なベン図は、Nが素数のときに限られるらしいです。ここでは、より一般の、対称性が低くてもいいので任意のNについてベン図を描くことを目標とします。

それでは、任意の自然数Nについて、Nベン図を描いていきましょう。

ベン図の双対グラフとハミルトン閉路

まずは準備のために、まずは、以下の補題を証明します。

補題 1

N ベン図の双対グラフにハミルトン閉路が存在するなら、N+1 ベン図が存在する。

ベン図の双対グラフとは、ベン図の線で区切られた各領域に1つずつ点(ノード)を描き、線1本を隔てる2つの領域の間に辺(エッジ)を結ぶことで得られる無向グラフのことです。

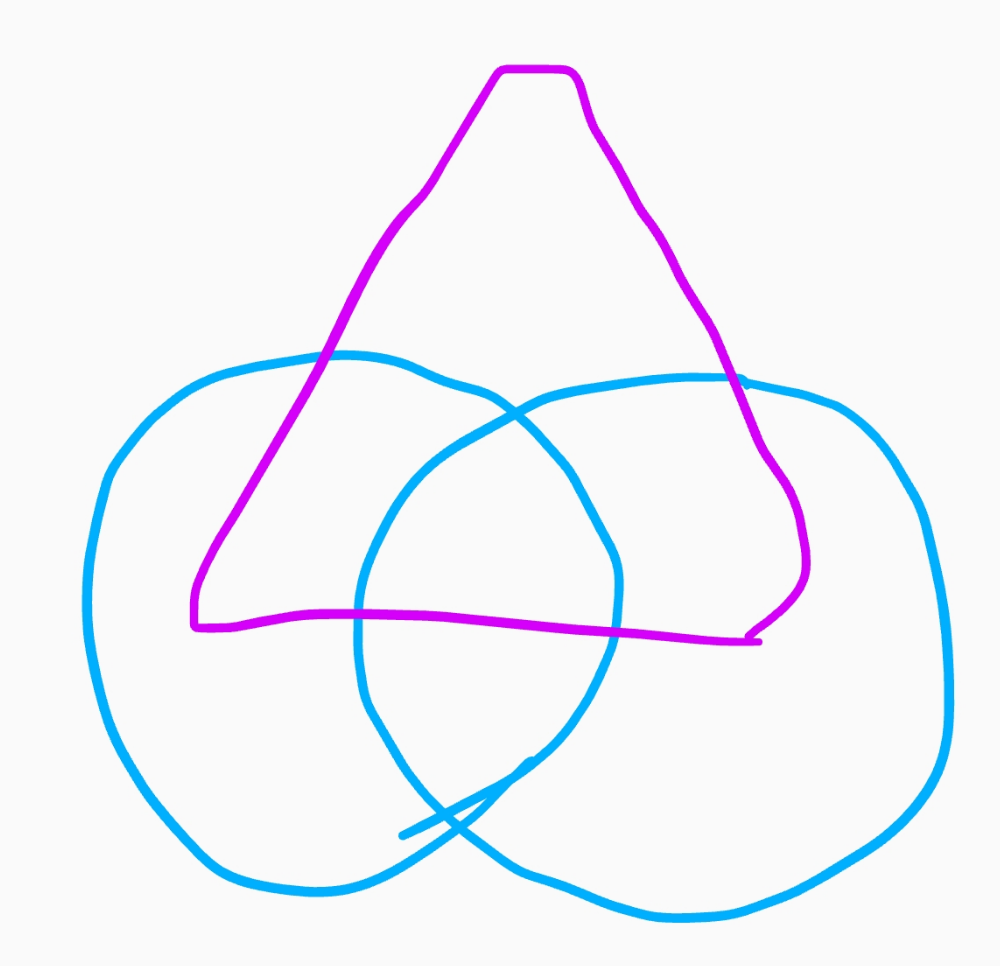
例えば、下図の青線で表される2-ベン図の双対グラフとは、黒丸のノードおよび黒線のエッジで表されるグラフです。

f:id:nunuki:20171231151949p:plain:w300

また、3-ベン図の双対グラフは次のようになります。

f:id:nunuki:20171231152152p:plain:w300

ハミルトン閉路とは、グラフの全てのノードを1度ずつ通る閉路のことです。

例えば、2-ベン図の双対グラフは、次のようなハミルトン閉路を持ちます。 (グラフ全体がハミルトン閉路になっています)

f:id:nunuki:20171231152331p:plain:w300

ここで、描かれたハミルトン閉路を新たな閉曲線とすると、3-ベン図ができます。

f:id:nunuki:20171231152421p:plain:w300

また、3-ベン図の双対グラフは、次のようなハミルトン閉路を持ちます。

f:id:nunuki:20171231152346p:plain:w300

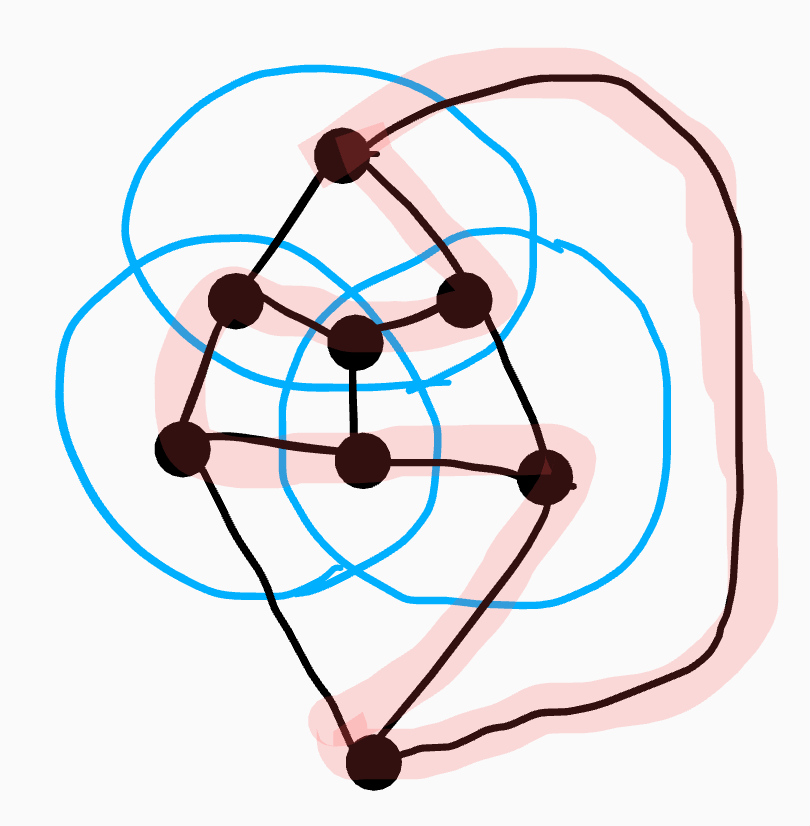
再び、ハミルトン閉路を新たな閉曲線とすると、4-ベン図ができます。

f:id:nunuki:20171231152443p:plain:w300

このように、Nベン図の双対グラフにハミルトン閉路が存在するとき、そのハミルトン閉路を新たな閉曲線とすると、N+1ベン図ができます。

なぜなら、Nベン図の双対グラフのハミルトン閉路は、 Nベン図の $2^{N}$ 個の領域を必ず1度ずつ通ります。このため、ハミルトン閉路は $2^{N}$ 個の各領域を2つに分割し、一方はハミルトン閉路の内側、もう一方は外側になります。したがって、ハミルトン閉路を追加することによって平面が各々異なる $2^{N+1}$ 個の領域に分割されることになり、 N+1ベン図ができることがわかります。

このように、Nベン図の双対グラフがハミルトン閉路を持つ場合、ハミルトン閉路を新たな閉曲線とすることで、 N+1 ベン図が得られることがわかりました。

問題は、このようなハミルトン閉路が、常に描けるかどうかです。

実は、一般のグラフが与えられたとき、そのグラフにハミルトン閉路が存在するか否かを判定する問題は、ハミルトン閉路問題と呼ばれ、NP完全という難しい(と信じられている)問題のクラスに属します。 *2

しかし、今対象としているのは一般のグラフではなく、 Nベン図の双対グラフという特殊な場合ですから、ハミルトン閉路が存在することを証明することができます。

このことを証明するために、「グレイコード」の性質を用います。

グレイコード

先ほどのNベン図の各領域に名前を付けます。ここでは、閉曲線の内側にあるならば1 外側ならば0を閉曲線の数だけ並べることで、各領域にN桁の2進数を対応させます。

例えば、3ベン図の各領域に名前をつけると、次のようになります。

f:id:nunuki:20171231153434p:plain:w300

ここで、1本の線で隔てられた2つの領域の数は、 2進表記の1桁だけが異なっていることがわかります。

つまり、先ほどの双対グラフのハミルトン閉路が通る領域の数を並べると、隣り合った数字が、2進表記の1桁だけが異なるような数列が出来上がります。

さて、ここで、グレイコード(Gray code) を導入します。

グレイコード $G_{n}$ とは、2進数の数列で、次の2つの条件を満たすものです。

$G_{n}$ には、2進表記n桁で表される $0 \sim 2^{n}-1$ の全ての数字が一度づつ現れる。
数列の隣り合った*3数字は、2進表記で1つの桁だけが異なる。

例えば、 $G_3$ は次のような長さ8の数列です。

これは、まさに、双対グラフのハミルトン閉路から作った数列と同じ形をしています！

以上のように、ベン図の双対グラフのハミルトン閉路がグレイコードに対応していることがわかりましたが、ここでは、逆に、グレイコードの性質を使うことで、実際にハミルトン閉路が引けることを証明したいと思います。

そのために、まずは、グレイコードのいくつかの性質を見ていきましょう。

グレイコードは、次のように再帰的に作ることができます。まず、 $G_{n}$ の各項を2回ずつ繰り返した、2倍の長さの数列を考えます。

次に、出来上がった数列の各数の右端に、0, 1, 1, 0, 0, 1, 1, ... を追加していくと、 $G_{n+1}$ ができます。

構成のしかたから明らかなように、 $m \leq n$ のとき、 $G _ {n+1}$ の各数の左からm桁目を集めた数列は、 $G _ {n}$ の各数の左からm桁目を集めた数列を2倍の長さにしたものになっています。

例えば、 $G_{3}$ の左から2桁目を縦に読むと、

[0,0,1,1,1,1,0,0,0]

ですが、 $G_{4}$ の場合、

[0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0]

となります。このように、 $G_{n}$ のm桁目の数字を集めた数列は、 nが変化しても、長さが変わるだけで、中身は本質的に変わりません。

ここで、この数列を横方向に縮め、連続区間 [0,1) で定義された関数 $g_{m}(x)$ で表します。つまり、

$g _ {m}(x) = \lim _ {n \rightarrow \infty } (G_{n}) _ { \lfloor 2^{n-1} x \rfloor }$

とします。

それでは、このグレイコードを使って実際にN-ベン図を構成していきましょう。

N-ベン図の構成

定理: N-ベン図の存在

実数 $\delta _ {1}, \cdots, \delta _ {N}$ が、 $1 > \delta _ {1} > \delta _ {2} > \cdots > \delta _ {N-1} > \delta _ {N} > 0$ を満たすとき、次の極座標表示で表される曲線 $C _ {1}, \cdots, C _ {N}$ はN-ベン図を成す。

$C _ {n}: r = 1 + \left(2g _ {n} \left( \frac {\theta} {2\pi} \right) - 1 \right) \delta _ {n} \;\;\; \cdots (1)$

ただし、非連続となる部分は動径方向に線分を引くことで連続な閉曲線にするものとする。

$C _ {n}$ の形は次のようになります。

f:id:nunuki:20171231155023p:plain 赤点線は半径1の円(単位円)です。

n が大きくなるなるにつれて、歯車型の曲線の歯の数が増え、歯の長さ(切込みの深さ)が小さくなっています。

各歯車は、グレイコードの1に対応する部分が出っ張って(半径が $1+\delta _ {n}$ )おり、 0に対応する部分が凹んで(半径が $1-\delta _ {n}$ )います。

これらを重ねることで、冒頭のツイートの図になります。

f:id:nunuki:20171231161217p:plain

ここで、赤点線で描いた単位円上のある一点を考えると、閉曲線のうち、出っ張っている物の内側、凹んでいる物の外側になっています。

例えば、図中の点Pは、 $C _ {3}, C _ {4}$ の内側、 $C _ {1}, C _ {2}, C _ {5}$ の外側になっています。

点Pを単位円周上で動かすと、グレイコードの性質から、内側・外側の全ての組み合わせが1回ずつ現れることがわかります。

つまり、上述の式(1) で表される図形がNベン図になっている場合、単位円は全ての領域を1度ずつ通る経路、すなわち、双対グラフのハミルトン閉路になっていることがわかります。

よって、補題1により、 $\{ C _ {1}, \cdots, C _ {N} \}$ がN ベン図になっているとき、これに単位円を追加したものはN+1 ベン図になっています。

ここで、N+1 個目に追加する図形は単位円でなくても、単位円に近い図形を選ぶことができます。

実際、単位円の代わりに $C _ {N+1}$ を追加する場合を考えると、 $0 \lt \delta _ {N+1} \lt \delta _ {N} \lt \cdots \lt \delta_ {1}$ ですから、 $C _ {N+1}$ の出っ張っている部分も凹んでいる部分も常に $C _ {1}, \cdots, C _ {N}$ より単位円に近いことになります。

したがって、 $C _ {N+1}$ は、単位円と同じ位置θ、つまり、 $C _ {1}, \cdots, C _ {N}$ が動径方向に変化している位置(凸凹の切り替わり = グレイコードの0と1の切り替わりの位置)でのみ $C _ {1}, \cdots, C _ {N}$ と交わることとなり、単位円の場合と同様の議論が可能です。

以上のことから、 $\{ C _ {1}, \cdots, C _ {N} \}$ がNベン図のとき、 $\{ C _ {1}, \cdots, C _ {N+1} \}$ もN+1ベン図であることが言えました。

1つの閉曲線は明らかに1-ベン図ですから、任意のNについて、 $\{ C _ {1}, \cdots, C _ {N} \}$ がベン図となっていることがわかりました。

まとめ

Nベン図からN+1ベン図を作る問題を、双対グラフのハミルトン閉路問題に帰着した。
グレイコードを使って、常にハミルトン閉路が描けるようなベン図を構成した。

*1: $\mathrm{int}(c)$ は単純閉曲線 $c$ の内部とする

*2:もし、ハミルトン閉路問題を多項式時間で解くアルゴリズムができた場合、全ての暗号通信が傍受可能になってしまうだけでなく、暗号通貨が盗み放題になってしまします。一方、ハミルトン閉路問題を多項式時間で解くアルゴリズムが存在しないことを証明した場合、アメリカのクレイ数学研究所から懸賞金の100万ドルがもらえます

*3:数列の末尾と先頭も隣り合っているものとする。

2016-12-23

半順序？弱順序？二項関係・順序関係まとめ

12/27更新: 図に文言を追加しました。

f:id:nunuki:20161227000205p:plain

半対称律?半順序?なにそれおいしいの?
Wikipediaを見てもよくわからない
半順序と弱順序を間違えて恥かいた

という方のために(?)、二項関係、順序関係についてまとめました。

特に、厳密な定義を意識せずに普段から二項関係を使っているであろうプログラマの方が少しでも理解・整理しやすいように解説しました。

TL; DR

集合Pに二項関係「」が定義されているとき、Pの異なる2要素x,y の関係は次の4つのどれか:
- x<=y が真(true)、かつ y<=x が真(true): 同値な関係
- x<=y が真(true)、かつ y<=x が偽(false): y は x より真に大きい
- x<=y が偽(false)、かつ y<=x が真(true): x は y より真に大きい
- x<=y が偽(false)、かつ y<=x が偽(false): x と y は比較不能
上記４つの関係を許すか禁止するかで次の５種類の二項関係が定義さている。
- 前順序: 真に大小、同値、比較不能すべてOK。
- 弱順序: 比較不能はNG。必ずどちらかが真に大きいか、同値な関係にある。
- 半順序: 同値な関係はNG。必ずどちらかが真に大きいか、比較不能である。
- 全順序: 比較不能も同値もNG。必ずどちらかが真に大きい。
- 同値関係: 真に大小はNG。必ず同値な関係か、比較不能のどちらか。
上記５つの二項関係には、さらに、２つの制約がある。
- 推移律: 「３すくみ」の関係は存在しない。
- 反射律: 各要素は自分自身と同値

二項関係

まず、ある集合Pの2項関係(P,≦)を考えます。すなわち、集合 Pに対して、次のような演算子が定義されていると考えてください。

bool operator <=(P x, P y);

さて、この演算子の戻り値はtrue かfalse の２つですが、二つの要素x, yが与えられたとき、その比べ方は x<=y とy<=x の2通りのがあります。

このとき、xとyの間には、x<=y およびy<=x の真偽の組み合わせで4通りの関係性があることがわかります。ここでは、便宜上、次のように呼ぶことにします。

x<=y	y<=x	名前
true	true	xとyは同値な関係
true	false	yはxより真に大きい
false	true	xはyより真に大きい
false	false	xとyは比較不能

ここで、「比較不能」や「同値」という関係が出てきましたが、実際の問題を考えるときには、これらの関係が現れると不都合なことがあります。

たとえば、配列のソートをしようとしたとき、比較不能な要素が現れるとどちらを先に並べてよいか困りますね？

また、「同値な関係」とは、たとえば、「AさんとBさんは違う人だが、年齢だけ見るとどちらも10歳で見分けがつかない」といった状況で、たとえば、小学校の名簿の中からAさんを探すときに、年齢を使って二分探索しようとすると、小学校に10歳の児童はたくさん居ますので、 Aさんを見つけることはできませんね。この場合、年齢ではなく、(学年, 出席番号) という組を辞書順で比較するような順序関係を考えると Aさんと学年と出席番号が両方等しい人は学校に居ませんから、Aさんを一意に見つけ出すことができます。

実は、弱順序、半順序、全順序 というのは、「比較不能」や「同値」が禁止されているということを意味しているのです。

このことを見ていく前に、まず、「比較不能」も「同値」も禁止されていない 前順序 の満たすべき性質についてまとめ、次に弱・半・全順序をまとめていきます。

反射律・推移律と前順序

最も条件の緩い順序関係である、前順序 (preorder)とは、「反射的かつ推移的な２項関係」のことです。

「反射的」「推移的」という新しい言葉が出てきましたが、これらは前順序をはじめ、全ての順序関係で成り立つべき性質です。

反射律

全てのx について、x <= x が成り立つ。

これは、xが自分自身と同値な関係にある ことを意味しています。

推移律

x <= y かつ y <= z ならば、x <= z が成り立つ。

これは、じゃんけんのような「3すくみ」のような関係が無いことを意味しています。 (グー <= パーかつ、パー <= チョキだが、グー <= チョキ は成り立たない。)

完全律と弱順序

既に述べた通り、前順序は「反射的かつ推移的な２項関係」ですが、「比較不能」や「同値」が禁止されていない最も緩い条件の順序関係でした。

弱順序 (total preorder; (non-strict) weak order) とは、「比較不能」を禁止する条件である「完全律」を前順序に課したものです。

完全律の定義は以下のとおりです。

完全律

全てのx, y について、x<=y またはy<=x のどちらか一方は真である。

この定義は、対偶をとると、

全てのx,yについて、「x<=yとy<=xがどちらも偽である」は偽である

となりますので、すなわち、

「xとyは比較不能である」となるx,y は存在しない

ということを言っています。

反対称律と半順序

次に、「同値な関係」を禁止しましょう。異なる２要素の同値な関係を禁止する条件を「反対称律」といい、前順序にこれを課した順序関係を半順序 (partial order) と言います。

反対称律

全てのx, y について、x<=y かつ y<=x ならば、a=b である。

この定義は

xとyが同値な関係ならば、x とy が等しい

ということですので、対偶を取れば

xとyが相異なる２要素ならば、xとyは同値な関係ではない

ということを言っているのが分かります。

全順序

さて、弱順序と半順序がそれぞれ「比較不能」と「同値な関係」を禁止した順序関係であることを述べました。

全順序 (total order) は、「比較不能」と「同値な関係」の両方を禁止した順序関係になります。

すなわち、２項関係 <= が全順序であるならば、相異なる２要素x, y は、必ずどちらかが真に大きいということです。

対称律と同値関係

さて、半順序とは「反対称律」を課した前順序であることを述べましたが、「反対称律」の「反」とはどういうことなのでしょうか？

「反」があるのだから、普通の「対称律」もあるのでは？という疑問が湧いてきます。

結論から言うと、「対称律」という条件も存在して、反対称律の代わりに対称律を課した前順序として「同値関係」という二項関係があります。

そもそも、反対称律とは、何が「反」なのでしょうか？

上述の反対称律の定義を再び変形していくと、

相異なるx,y について、y<=x が真なら、x<=y は偽である。

となります。

「y<=x が真なら、x<=y は偽である」の部分を見ると、「xとyの順番を入れ替えると、真偽が入れ替わる」ということを意味しています。これが「反」対称と言われる所以です。

では、対称律はどうなっているでしょうか？

対称律

全てのx, y について、x<=yが真ならば y<=xも真である。

つまり、「xとyの順番を入れ替えても、真偽は変わらない」と言っているのです。

ここで、対称律には「相異なるx,y について」という条件がありませんが、 xとyが等しいとき、x<=x の「xとxの順番」を入れ替えても、真偽が変わらないのは当たり前ですから、書く必要が無いのです。

さて、対称律が成り立っているとき、 x<=yまたはy<=xのどちらかが成り立つと、自動的にもう一方も成り立ちますから、「xとyのどちらかがもう一方よりも真に大きい」という状況は起こりません。

つまり、対称律を課した順序関係である「同値関係」とは、とは、2つの要素間で「どちらかが真に大きい」という関係を禁止し、「同値な関係」または「比較不能」の２種類の関係だけを許す二項関係のことなのです。

また、同値関係では、x<=y とy<=x を区別する必要がありませんから、通常 $\leq$ という記号は用いず、 $x \sim y$ といった記号を用いることが多いです。

まとめ

順序関係(前順序)とは

反射的(各要素は自分自身と同値)で推移的(３すくみがない)な２項関係

のことでした。

このような二項関係で相異なる２要素 x, y を比較した時、 x<=y とy<=x の真偽の組み合わせによって４つの関係性（xが真に大、yが真に大、xとyは同値、xとyは比較不能）があります。

これら４つの関係性のうち、いくつかを禁止する条件を加えることによって５種類の二項関係を得ました。

	真に大小	同値な関係	比較不能
禁止する条件	対称律	反対称律	完全律
前順序	◯	◯	◯
弱順序	◯	◯	×
半順序	◯	×	◯
全順序	◯	×	×
同値関係	×	◯	◯

最後に、これらの包含関係をまとめておきます。

f:id:nunuki:20161227000205p:plain

2016-11-20

無限長の配列はソート可能か？

皆さんご存知の通り、有限サイズの任意の配列は、有限回の比較と交換でソートすることができます。 (挿入ソートやクイックソートなどの具体的なアルゴリズムが存在することが、その証明になっています)

では、配列が無限の長さを持っていた場合はどうなるでしょうか？

Twitter で考えたことをまとめます。

ソート可能性

ソートとは、配列の各要素が演算子 $\leq$ 比較可能なときに、各要素が「下から何番目か」という番号を振ることであると考えられます。

そこで、有限配列のソート可能性を次のように定義します。

定義: 有限集合のソート可能性

有限な順序集合 $(X, \leq)$ について、任意の全単射 $\phi: X \rightarrow \{1, \cdots, | X | \}$ に対して次の２つを満たす全単射 $\psi: \{1, \cdots, | X | \} \rightarrow \{1, \cdots, | X | \}$ が存在するとき、 $X$ はソート可能であるという。

$x \leq y \Leftrightarrow \psi(\phi(x)) \leq \psi(\phi(y))$

$\psi$ は有限個の互換の合成で表される。

上の定義で、 $\phi$ はソート前の配列を表し ( $x \in X$ は $\phi(x)$ 番目の要素)、 $\psi$ がソートによって「n番目の要素が $\psi(n)$ 番目に移動する」ことを表しています。

ここで、1つ目の条件は、 $X$ と $\{1, \cdots, | X | \}$ が順序同型であるということを意味します。要素数が等しい任意の有限集合は順序同型ですから、これは常に成り立ちます。

また、２つ目の条件についても、任意の有限置換は互換の積で表されますから、こちらも常に成り立ちます。

これらのことから、任意の有限集合はソート可能であることが確認できました。

(この定義のみからでは、有限回の比較回数で $\psi$ を構成可能であるかどうかについては触れていないのでご注意ください。このあたりの精緻な議論は私の手に余ります。。。)

それでは、ソート可能性の概念を無限長の配列に拡張しましょう。

定義: 可算無限集合のソート可能性

可算な順序集合 $(X, \leq)$ について、任意の全単射 $\phi: X \rightarrow \mathbb{N}$ に対して次の２つを満たす全単射 $\psi: \mathbb{N} \rightarrow \mathbb{N}$ が存在するとき、 $X$ はソート可能であるという。

$x \leq y \Leftrightarrow \psi(\phi(x)) \leq \psi(\phi(y))$

$\psi$ は可算個の互換の合成で表される。

はい、有限を可算無限にしただけですね。しかし、一般に可算無限集合に対しては、ソート可能性は成り立ちません。

たとえば、可算無限個の要素からなる配列

$\displaystyle X = \left( \frac{(-1)^{i}}{i} \right) = \left(-1, \frac{1}{2}, -\frac{1}{3}, \frac{1}{4}, \cdots \right)$

を通常の意味の大小関係でソートする場合を考えましょう。

f:id:nunuki:20161120004037p:plain

もし、 $X$ がソート可能であると仮定すると、 $X$ の最小・最大の要素 $-1, \frac{1}{2}$ のソート後の順番がそれぞれ $m,n$ と求まります。

すると、 $X$ の要素数は $n-m+1$ 個となってしまいますが、これは、 $X$ が無限集合であることと矛盾します。よって、 $X$ はソート不可能であることがわかりました。

これは、条件1の「可算無限集合 $X$ は自然数全体の集合 $\mathbb{N}$ と順序同型である」が一般には成立しないことを反映しています。

逆に言えば、 $X$ がソート可能であるためには、 $X$ が $\mathbb{N}$ と順序同型であることが必要です。

このための必要条件として、

$X$ は最小値を持つ
$X$ は最大値を持たない
$X$ の任意の２要素 $a \leq b$ について、 $X$ の部分集合 $\{ x\in X | a \leq x \leq b \}$ は有限集合である

などが挙げられますが、他にもいろいろと条件がありそうです。

この議論を進めていくと、整列順序など、数学の基礎的な概念の話になってくるようですが、こちらはまだまだ勉強不足です。

2016-11-19

日立のレンズレスカメラの原理を考察してみた

日立のレンズレスカメラ

つい先日、日立がレンズが不要な新しい原理のカメラを発表しました。

ニュースリリース：2016年11月15日：日立

従来型のカメラは、レンズの焦点距離の存在により、薄型化に原理的な限界があるのに対し、新しい原理を用いることで、格段に薄いカメラが実現可能になります。

このカメラは、撮像素子の表面1mmのところに同心円状のパターンを印刷したフィルムを配置するという簡単な構造をしています。

撮像後の画像に、フィルムと同じパターンを重ねることでモアレ(干渉縞)を発生させ、その縞模様をフーリエ変換によって抽出することで、画素を作っているようです。

パターンを印刷したフィルムを使ったレンズレスカメラ自体は、以前から知られているようで、

ASCII.jp：レンズなしで画像を撮影できる新技術「FlatCam」

今回の日立の技術のポイントは、この同心円状のパターンを使うことによって、

フーリエ変換(FFT)で高速に画像が復元できる
パターンのサイズを変えることによってピントを撮影後に調整できる

という2点のようです。

特に、前者の特徴を持つような同心円状のパターンとはどのようなものなのでしょうか？実際に計算してみましょう。

同心円パターンの導出

2つの同心円パターンの作る干渉縞

下図のような配置を考えます。

f:id:nunuki:20161117232709p:plain

平面 $z=0$ 上に撮像素子があり、そこから距離 $l$ だけ離れた $z=l$ にフィルムを置きます。無限遠点の1点から発せられた光は、平行光として入射角 $\theta$ でフィルムに入射します。

平行光によるフィルムの像は、もとの位置から $x=d \approx l \theta$ だけずれて撮像素子に写ります。撮影した画像に、画像処理でフィルムと同じパターンを重ねることで(図のフィルム２)、干渉縞が現れます。この干渉縞が並行波になるためには、どのようなフィルムのパターンを用いればいいか、考えていきましょう。

いま、フィルムのパターンが次の条件を満たすと仮定します。

同心円状(点対称)な図形であること
縞模様 (透過率が値が、0と1の間で連続的に反復する) であること

すなわち、フィルムの透過率が、フィルムの中心からの距離 $r$ の関数として、

$\displaystyle f(r) = \frac{1}{2} ( 1+\cos \phi ( r ) ) = \cos^{2} \frac{\phi (r)}{2}$

と表されるとします。ただし、 $\phi(r)$ は微分可能な単調増加関数です。

f:id:nunuki:20161118000949p:plain

ここで、撮像素子の平面上の点 $(x,y)$ を考えると、

フィルム1の像のパターンの中心からの距離: $r_{1} = \sqrt{(x-d)^{2}+y^{2}}$
フィルム2(撮影後の画像処理)のパターンの中心からの距離が $r_{2}=\sqrt{x^{2}+y^{2}}$

ですから、この点における光の強度は、

$\displaystyle F = f(r_1) \cdot f(r_2) = {\left( \cos \frac{\phi (r_1)}{2} \cos \frac{\phi (r_2)}{2} \right)}^{2} = \frac{1}{4} \left( \cos \frac{\phi (r_2) + \phi (r_1)}{2} + \cos \frac{\phi (r_2) - \phi (r_1)}{2} \right)^{2}$

となります。最後の等号は三角関数の積和の公式を使いました。

ここで、２つのパターンの中心からの距離の差 $\Delta r$ は、 $d \ll r_{1}$ のとき、

$\displaystyle \Delta r = r_{2} - r_{1} = \sqrt{x^{2}+y^{2}} - \sqrt{(x-d)^{2}+y^{2}} \approx \frac{xd}{2r_{1}}$

となるので、

$\displaystyle \phi ( r_{2} ) = \phi ( r_{1} + \Delta r ) \approx \phi ( r_{1} ) + \Delta r \phi' ( r_{1} )$
$\displaystyle \cos \frac{\phi (r_2) + \phi (r_1)}{2} \approx \cos \phi( r_{1} )$
$\displaystyle \cos \frac{\phi (r_2) - \phi (r_1)}{2} \approx \cos \Delta r \phi' ( r_{1} )$

となり、最終的に、

$\displaystyle F \approx \frac{1}{4} \left( \cos \phi( r_{1} ) + \cos \frac{xd\phi' ( r_{1}) }{2r_{1}} \right)^{2}$

を得ます。

並行波があらわれる条件

上の式で、カッコ内の第1項はもともとのフィルター1のパターンを表しています。

注目すべきは第2項で、これが干渉縞を表しています。この干渉縞が並行波になるためには、 $\frac{xd \phi' ( r_{1} )}{2 r_{1}}$ が $x$ に比例すれば良いことがわかります。このためには、 $\frac{ \phi' ( r_{1} ) }{r_{1}}$ が定数でなければならず、

$\displaystyle \frac{ \phi' ( r ) }{r} = C$

$\displaystyle \therefore \phi ( r ) = C r^{2} + \phi_0$

$\displaystyle \therefore f ( r ) = \cos^{2} \frac{C r^{2} + \phi_0}{2}$

のように、同心円パターンの具体的な表式が求まりました。

これは、波長(縞の間隔) $\lambda = \frac{1}{Cr}$ が中心からの距離に反比例して小さくなる縞模様であることを意味しています。

さらに、 $\frac{Cl}{2} = k_{0}$ とすれば、

$\displaystyle f ( r ) = \cos^{2} \left( \frac{k_{0} r^{2}}{l} + \frac{\phi_{0}}{2} \right)$

となり、このときの干渉縞の波数は $\frac{d \phi' ( r_{1} )}{2 r_{1}}=\frac{k_{0}d}{l} \approx k_{0} \theta$ となることがわかります。

数値実験

では、上で求めた同心円パターンが作る干渉縞を実際に観察してみましょう。

f:id:nunuki:20161119193950p:plain

上の画像で、左は元のパターン、真ん中は中心を右下に少しずらしたパターン、右はこれら２つを重ねたものになっています。

確かに並行波のパターンが現れていることがわかります。この干渉縞をフーリエ変換したものが、下図になります。

f:id:nunuki:20161119195003p:plain

図の左上付近の位置に輝点が現れています。平行光の差し込む角度と方向によってこの輝点の位置が変わります。

実際にこのカメラで画像を撮ると、様々な角度・方向から差し込む光がそれぞれの位置につくる輝点の集合が元の画像を復元します。

まとめ

日立のレンズレスカメラの原理について考察しました。

レンズの代わりに用いられているフィルムに描かれる同心円上のパターンは、中心からの距離に反比例して縞の間隔が狭くなるものであることがわかりました。このパターンを用いることで、干渉縞が並行波となり、フーリエ変換で光の差し込む角度・方向を取得することができることがわかりました。

次回は、気が向いたら、撮影後のピント調整の原理と、被写体深度について考えてみようかな。